Understanding Option Pricing: A Comprehensive Guide to Intrinsic and Time Values of Options

How are Options Priced?

The market forces affecting the value of the underlying asset will in turn affect the market value of the options attached to that asset. The option itself has no underlying value, its value is derived from the asset itself and your ability to buy or sell that asset.

The Fundamentals of Option Pricing

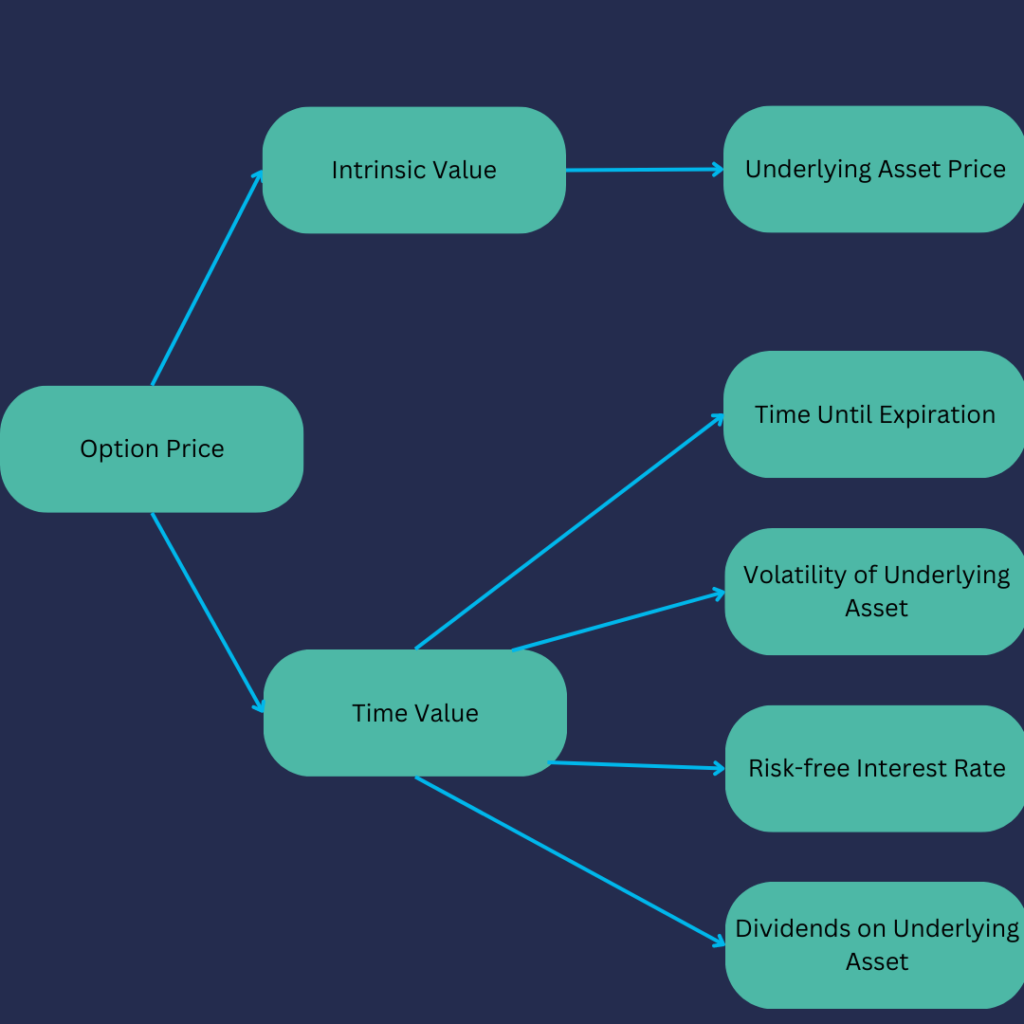
Understanding Options premium is key to options trading. There are two fundamental components of an option price. These components are intrinsic value and time value.

Option Price = Intrinsic Value + Time Value

Intrinsic Value of Options

Intrinsic value represents the immediate, tangible value of an option. It is the profit that could be made if the option were exercised right now. 

Intrinsic value exists when an option is in the money. 

For a call option, the intrinsic value is the difference between the underlying asset’s market price and the strike price, given it is in a profitable position (i.e. the market price is above the strike price). 

For a put option, the intrinsic value is the difference between the strike price and the underlying asset’s market price, provided the market price is below the strike price. 

When the option is ‘out-of-the-money’ (not in a profitable position), the intrinsic value is zero, as exercising the option would not yield profit. 

If you own an option to buy stock XYZ Plc at 400 (a call) and the current market price of the stock is 420, then you would expect that your option would be worth at least 20. The intrinsic value of the option arises because the option gives you the right to buy the stock at 20 less than the current market value of the stock. 

In regard to a put, if you bought the 400 put option in XYZ Plc and the market is trading at 375 then the option has an intrinsic value of 25. 

In-the-money Options

Options that have intrinsic value in their pricing are referred to as being ‘in-the-money’. For call options, this means that the strike price of the option is below the current market value of the underlying asset and so there is value in exercising the option. The intrinsic value is present as the option holder can exercise their option and buy the underlying shares for a price lower than they could in the market. 

The calculation of intrinsic value for put options is the same as for call options, except that intrinsic value for put option prices is present when the strike price of the option is above the current market value of the underlying asset.

Out-of-the-money Options

Options that have no intrinsic value in their pricing are referred to as being ‘out-of-the-money’. For call options, this means that the strike price is above the current market value and so there is no value in exercising the option. 

At-the-money Options

As the name suggests, an at-the-money option is an option whereby the strike price of the option is equal to the current market value of the underlying shares. The option premium has no intrinsic value but will have time value. 

Time Value

Time value is a little more difficult to understand than intrinsic value. It is the portion of an option’s price that exceeds its intrinsic value. It accounts for the possibility that the option may become ‘in-the-money’ (in a profitable position) before its expiration date. 

The time value of an option is influenced by several factors, such as the volatility of the underlying asset, the time remaining until expiration, the risk-free interest rate, and any dividends due on the underlying asset. 

Time value in options will vary with in-the-money, out-of-the-money and at-the-money options. This is because each of these scenarios presents different opportunities and probabilities of an increase in the intrinsic value of an option. Generally, time value is greatest on at-the-money options, as the risk for the seller is highest here that it could go in your direction. 

Time Value is influenced by the following factors;

• Time to Expiry: 

The first factor affecting the time value of an option is time itself. The more time you have in which to achieve the market movement you expect, the greater the chance is of it happening so, the longer the time period left on an option, the greater the time value will be. 

As the expiry of the option gets closer, the time value diminishes with every day that passes. Time value also does not reduce at a constant rate, it reduces at a faster rate the closer you get to the expiry date. 

• Volatility: 

Volatility is the range and speed at which a price moves. When a price moves a lot within a relatively short amount of time, it is said to have high volatility. The greater the volatility of the underlying asset, the greater the time value of the option that will exist. 

• Dividend Payments: 

When trading options, it is the ex-dividend date that is important. The ex-dividend date is the day on which all shareholders who own shares at the end of trade on that day will be entitled to the dividend payment. The next day, the share price usually falls by an amount similar to the dividend amount, as anyone who buys shares on that day will not be entitled to the dividend. 

Options do not grant you any rights to dividends in the underlying shares. When choosing an option, you should always consider any dividends payable. If the underlying share has an ex-dividend date during the life of your option, this will affect the intrinsic value of the option, without the option holder having any rights to any dividends. Any ex-dividend amounts will be priced into the intrinsic value. 

The Interplay Between Intrinsic and Time Values

Intrinsic and time values are interrelated, and their interplay is essential for understanding how option prices fluctuate.

Options with more time until expiration have a higher time value, as they provide more opportunities for the option to become profitable. As the expiration date approaches, the time value decreases—a phenomenon known as ‘time decay.’

In contrast, intrinsic value does not decay over time. It changes only with fluctuations in the underlying asset’s price.

Implications for Options Trading

Understanding the intrinsic and time values of options can significantly enhance your options trading strategy. 

Traders looking to profit from short-term price volatility might focus more on options with a high time value, while those interested in the long-term potential of the underlying asset might consider options with substantial intrinsic value. 

In conclusion, by understanding the intrinsic and time values of options, traders can better predict potential profits and losses, optimise their trading strategy, and make more informed decisions.

Understanding the Greeks in Options Trading

In options trading, the ‘Greeks’ are statistical values that provide traders with a way to measure the sensitivity of an option’s price to a range of factors. They include Delta, Gamma, Theta, Vega, and Rho. 

Delta

Delta measures how much an option’s price is expected to change per $1 change in the price of the underlying asset. 

Gamma

Gamma measures how much the Delta is expected to change per $1 change in the price of the underlying asset. 

Theta

Theta measures the rate of decline in the value of an option due to the passage of time. 

Vega

Vega measures the change in the price of an option for every 1% change in the underlying asset’s implied volatility. 

Rho

Rho measures the sensitivity of an option’s price to changes in the interest rate. 

Understanding the Greeks can help traders manage risk and make more informed decisions about their options trading strategies.

Volatility and Its Impact on Option Pricing

Volatility, a measure of the degree of variation in the price of an underlying asset over time, is a crucial factor in options pricing. Higher volatility generally increases the price of options, as it implies a greater probability for substantial price moves, which could make the option more valuable.

Volatility comes in two forms: historical and implied. Historical volatility refers to the fluctuation in an asset’s price in the past, while implied volatility, derived from an option’s price, reflects the market’s expectation of future price volatility.

Options Pricing Summarised

Option pricing involves two primary components: intrinsic value and time value. The intrinsic value refers to the tangible, immediate profit that could be made if the option were exercised at the current time. It is the difference between the underlying asset’s market price and the strike price, provided the option is in a profitable position.

The time value is the part of an option’s price that goes beyond its intrinsic value. It represents the potential that the option might become profitable before its expiration. This value is influenced by numerous factors, including the time remaining until expiration, the volatility of the underlying asset, the risk-free interest rate, and any dividends due on the underlying asset.

Together, the intrinsic value and time value make up the total value or price of an option. Understanding these concepts is crucial for traders to make informed decisions in options trading.