The Greeks - Understanding Gamma Options

Gamma Options Explained

Gamma is the expected change of an option’s delta given a 1 unit move in the underlying asset price. It is expressed as a percentage and like the delta, it is constantly changing with every point move of the underlying asset. Since delta is an important measure, options traders are very interested in the rate of change of this and therefore gamma is calculated.

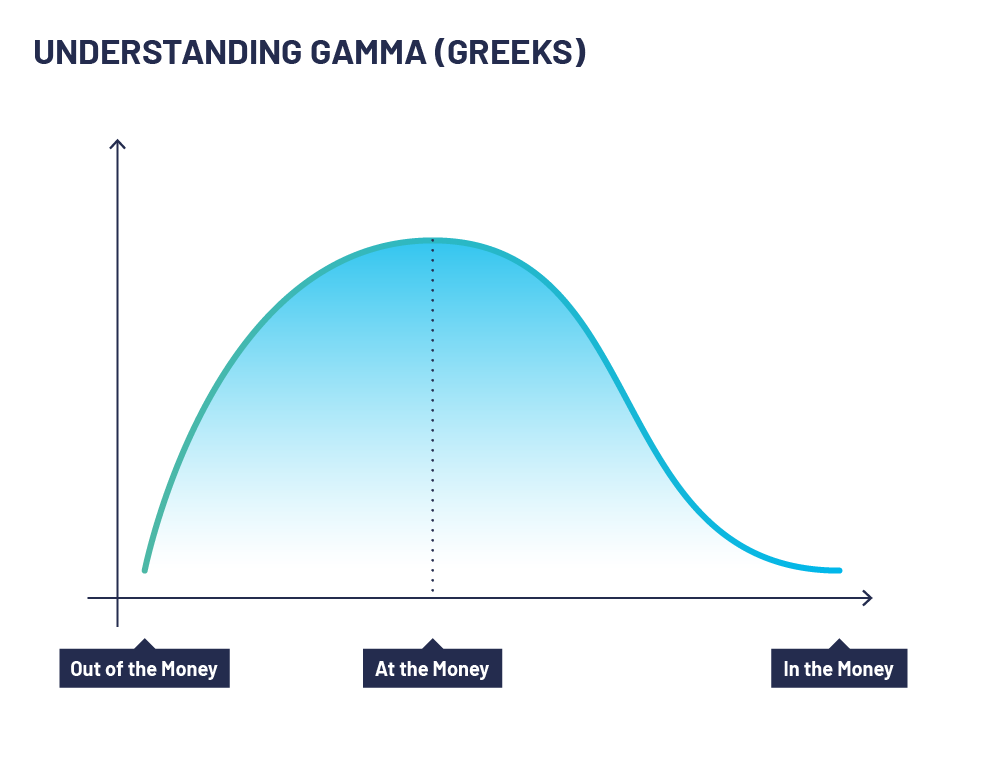
As the underlying moves away from the strike price, gamma decreases. As the underlying moves towards the strike price, the gamma increases.

At-the-money options have the highest gamma because their deltas are the most sensitive to underlying price movements.

Looking at the table we can see a call has a delta of +0.50 and then a gamma of +0.10. If the underlying asset price moves up 1 unit then the delta is expected to move to +0.60 and therefore if it goes down 1 unit the delta should move to a +0.40. Gamma can be read as the rate of change of the probability of an option expiring at the options strike price. 

How is Gamma Calculated?

Delta1 – Delta2  = γ (Gamma)

       P1 – P2

P = underlying asset price

Essentially, Gamma is calculated by dividing the change in delta by the change in price.